Em pesquisas, frequentemente, procura-se verificar se existe relação entre duas ou mais variáveis, isto é, saber se as alterações sofridas por uma das variáveis são acompanhadas por alterações nas outras. Por exemplo,
peso vs. idade, consumo vs. renda, altura vs. peso, de um indivíduo.
O termo correlação significa relação em dois sentidos (correlação), e é usado em estatística para designar a força que mantém unidos dois conjuntos de valores. A verificação da existência e do grau de relação entre as variáveis é o objecto de estudo da correlação.
Uma vez caracterizada esta relação, procura-se descrevê-la sob forma matemática, através de uma função. A estimação dos parâmetros dessa função matemática é o objecto da regressão.
Os pares de valores das duas variáveis poderão ser colocados num diagrama cartesiano chamado “diagrama de
dispersão”. A vantagem de construir um diagrama de dispersão está em que, muitas vezes sua simples observação já nos dá uma ideia bastante boa de como as duas variáveis se relacionam.
Exemplo: Renda x Anos de estudo
As correlações variam com respeito a sua força. Podemos visualizar essa força num diagrama de dispersão que é um gráfico capaz de mostrar a maneira pela qual os valores de duas variáveis, X e Y, distribuem-se ao longo da faixa dos possíveis resultados.
Portanto, do gráfico acima pode-se notar que a força da correlação entre X e Y aumenta a medida que os pontos se agrupam em torno de uma linha reta imaginária.
Tipos de Correlação ( Correlação Positiva, Negativa e Curvilínea)
O diagrama de dispersão mostrará que a correlação será tanto mais forte quanto mais próximo estiver o
coeficiente de –1 ou +1, e será tanto mais fraca quanto mais próximo o coeficiente estiver de zero.
a) Correlação perfeita negativa (rxy = -1): Quando os pontos estiverem perfeitamente alinhados, mas em sentido contrário, a correlação é denominada perfeita negativa.
b) Correlação negativa (-1 < rxy < 0): A correlação é considerada negativa quando valores crescentes da variável X estiverem associados a valores decrescentes da variável Y, ou valores decrescentes de X associados a valores crescentes de Y.
c) Correlação nula (rxy = 0): Quando não houver relação entre as variáveis X e Y, ou seja, quando os valores de X e Y ocorrerem independentemente, não existe correlação entre elas.
d) Correlação positiva (0 < rxy < 1): Será considerada positiva se os valores crescentes de X estiverem associados a valores crescentes de Y.
e) Correlação perfeita positiva (rxy = 1): A correlação linear perfeita positiva corresponde ao caso anterior, só que os pontos (X, Y) estão perfeitamente alinhados.
Relação entre duas variáveis quantitativas.
Se retirarmos de uma população, uma amostra casual de tamanho N, teremos para cada elemento da amostra um par de observações: um valor de X e um valor de Y. Esses pares determinam N pontos no plano que podem ser representados graficamente num sistema de eixos cartesianos.
Ao gráfico acima dá-se o nome de diagrama de dispersão, esses nos fornece uma idéia intuitiva da eventual relação entre as duas variáveis.
Pode-se medir essa correlação através do Coeficiente de Correlação Linear de Pearson (r):
onde r varia entre -1 e 1
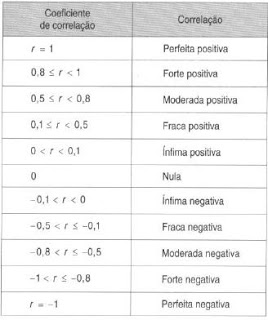
Coeficiente de Correlação (C)
Expressa numericamente a força e o sentido da correlação. Os coeficientes oscilam entre -1 e 1.
OBSERVAÇÕES:
- Correlação não é o mesmo que causa e efeito. Duas variáveis podem estar altamente correlacionadas e, no entanto, não haver relação de causa e efeito entre elas.
- Se duas variáveis estiverem amarradas por uma relação de causa e efeito elas estarão, obrigatoriamente, correlacionadas.
- O estudo de correlação pressupõe que as variáveis X e Y tenham uma distribuição normal.
- A palavra simples que compõe o nome correlação linear simples, indica que estão envolvidas no cálculo somente duas variáveis.
- O coeficiente de correlação linear de Pearson mede a correlação em estatística paramétrica.
- Coeficiente de correlação de Spearman (correlação por postos}é o correspondente à área não paramétrica..
Exercício Pratico
De acordo com o resultado podemos concluir que existe uma relação forte entre as notas das duas disciplinas, ao seja, os alunos com melhores notas em Matemática tendem a ter melhores notas na disciplina de estatística.